Şansın adil testlerde oynayabileceği rolün değerlendirilmesi
Şansın rolü, adil tedavi kıyaslamalarının yorumlanmasında bizi iki çeşit hata yapmaya itebilir: tedavi sonuçlarında olmamasına rağmen gerçek farklılıklar olduğu sonucuna varabilir ya da var olan farklılıkların olmadığı sonucuna varabiliriz. Gözlemlenen tedavi sonuçları ne kadar fazlaysa, bu şekilde yanılma ihtimalimiz o kadar azalacaktır.
Çünkü tedavi kıyaslamaları, tedavi edilebilen duruma sahip olan/olacak herkesi kapsamaz, tedaviler arasındaki “gerçek farklılıkları” mutlak surette bulmak mümkün olmayacaktır. Bunun yerine, çalışmalar gerçek farklılıkların neler olabileceğine dair en iyi tahminleri üretmek zorundadır.
Tahmini farklılıkların güvenilirliği, genellikle “Güven Aralıkları” (GA) ile gösterilir. Bu aralıklar, gerçek farklılıkların hangi aralıkta yayılabileceğini gösterir. Pek çok kişi, bu isimle olmasa bile güven aralıkları kavramına zaten aşinadır.
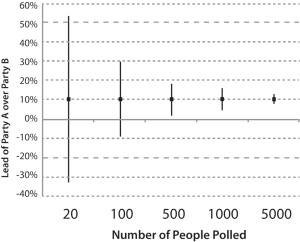
Örneğin, seçimlerden hemen önceki bir fikir anketi A Partisinin B Partisinin yüzde 10 puan ilerisinde olduğunu belirtebilir ancak bu rapor daha sonra genellikle gruplar arasındaki farkın 5 puan kadar az ya da 15 puan kadar çok olduğunu da belirtecektir. Bu “güven aralığı” gruplar arasındaki gerçek farkın yüzde 5 ila 15 puan arasında bir yerlerde dağılım gösterdiğini belirtir.
Ankete katılan kişi sayısı ne kadar çoksa, sonuçlarla ilgili belirsizlik o kadar az olacaktır; bu yüzden fark tahmini ile ilgili güven aralığı da o kadar dar olacaktır.
İki siyasi partiyi destekleyen seçmenlerin oranlarındaki tahmini farkın belirsizlik değeri ölçülebileceği gibi, iki tedavi sonrasında iyileşen veya kötüleşen hastaların oranlarındaki tahmini farklılığa ilişkin belirsizlik derecesi de ölçülebilir.
Yine bu noktada, gözlemlenen tedavi sonuçları ne kadar fazlaysa, örneğin kalp krizi sonrası iyileşme gibi, iki tedavi arasındaki kıyaslamada, tedavi farklılıklarının tahminleriyle ilgili güven aralıkları o kadar dar olacaktır. Güven aralıklarıyla ilgili olarak “ne kadar darsa, o kadar iyidir” denebilir.
Bir güven aralığı genellikle, doğru değerin sunulan tahmin aralığında bulunacağından ne kadar emin olduğumuzun bir göstergesidir. Örneğin, “%95’lik güven aralığı”, tahmin edilen doğru değerin güven aralığında bulunmasından %95 emin olduğumuz anlamına gelir. Yani aslında “doğru” değerin aralık dışında kalma şansı 100’de 5 ihtimaldir (%5).
The 95% Confidence Interval (CI) for the difference between Party A and Party B narrows as the number of people polled increases (click to enlarge).